Sir Francis Galton

 Galton, el hombre que medía todo

Sir Francis Galton (1822-1911) fue un hombre polifacético fue : antropólogo, biólogo, geógrafo, meteorólogo, explorador, inventor, psicólogo, eugenista británico y estadístico. Destacó desde pequeño pues a los dos años y medio aprendió a leer y a los cinco podía leer cualquier libro en inglés con tremenda soltura. En su historial académico de juventud sobresalió especialmente en matemáticas, no brillando excesivamente en las demás áreas. Al enorme valor de sus investigaciones hay que añadir el hecho de que las hizo siempre por su cuenta ya que nunca tuvo un puesto en ninguna universidad. No es menos cierto que procedía de una familia acomodada y nunca pasó por apuros económicos. Las ideas de Galton fueron tan brillantes e influyentes que abrieron el camino a lo que hoy son varias disciplinas diferentes.

Era primo por parte de madre de Charles Darwin y los planteamientos sobre la evolución de éste condicionaron en  gran medida los intereses investigadores de Galton, las inteligentes preguntas que se hizo y las magníficas respuestas que se dio.

Fundó junto con sus discípulos Karl Pearson y Walter Weldon la revista Biometrika para promover el estudio de la Bioestadística (aún vigente hasta el 2004).

Regresión a la media y  Galton

Galton  sentó las bases de la ciencia que hoy conocemos como Estadística. Fue el primero en estudiar la vinculación entre variable introduciendo el uso de la recta de regresión y explicando el fenómeno de la regresión a la media en un artículo de finales del siglo XIX. En este trabajo Galton estableció una relación de tipo lineal entre la altura de los padres y la de los hijos, enfatizando el hecho de que los hijos de padres altos son, en media, de menor estatura que sus padres, y que los hijos de padres bajos son, en promedio, más altos que sus padres. Inicialmente este fenómeno recibió el nombre de regresión (vuelta atrás) a la mediocridad y hoy lo conocemos como regresión a la media. La regresión a la media es observable con frecuencia en nuestras vidas y nos referimos a ella en múltiples situaciones quizá sin conocer la terminología científica. Cuántos de los alumnos y profesores, brillantes académicamente desde su infancia, se han frustrado porque sus hijos no tienen mayor rendimiento académico. Sin embargo, los padres que no acabaron el bachillerato tienen en media hijos que les superan en formación. Solemos decir con frecuencia en referencia a la continuación de una película que nos deslumbró: “Segundas partes nunca fueron buenas”. Esta afirmación se puede explicar en términos de la regresión a la media. Si representamos en una nube de puntos las taquillas de la primera y de la segunda parte (utilizando la recaudación como una medida de calidad, lo cual puede ser desde luego discutible) en general, podremos observar el fenómeno. Entre las primeras partes cuya recaudación fue muy alta, la de las segundas partes, en promedio será menor. Pero también lógicamente hay segundas partes que fueron mejor que la primera y eso muchas veces ocurre cuando la primera fue menos exitosa. Similarmente, si nos trasladamos al entorno del deporte, los efectos que Galton detectó en las relaciones entre la altura de padres e hijos se pueden observar en la transmisión de la habilidad. El hijo de Messi o el de Cristiano tiene muy difícil superar el listón que le va a dejar su padre y será, si se dedica a ello, casi con toda seguridad, un futbolista menos dotado. En nuestro entorno de investigación, todos nos hemos sorprendido alguna vez por la que considerábamos escasa calidad de un artículo publicado en una revista de alto impacto. Rousseeuw (1991) analiza el fenómeno. Si un artículo es revisado por tres referís y estos emiten una valoración muy positiva del artículo, el editor decidirá su publicación. Ahora bien, si ese mismo artículo es revisado a continuación por otros tres evaluadores, en promedio, la valoración será menor. Y si acudimos a nuestro entorno docente, con frecuencia comentamos con compañeros por los pasillos que “el grupo actual no fue de lo mejor, respecto de lo bueno que fue el del año pasado”. O también: “menos mal que los alumnos de este año no son tan malos como los del año pasado”.

Retrato de Charles Wellington Furse , 1903

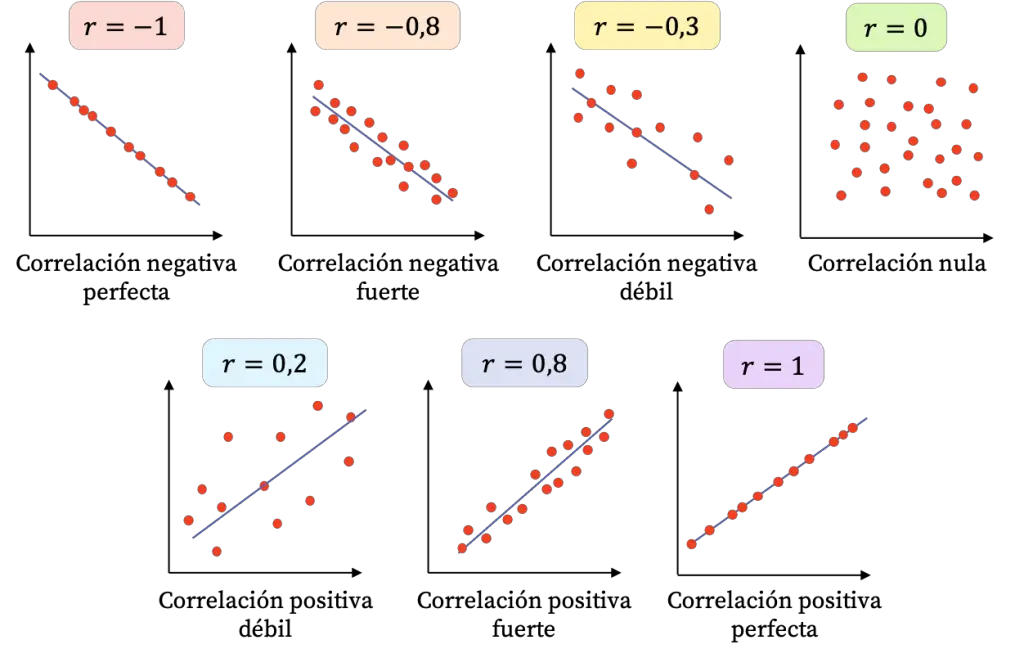
Coeficiente de correlación lineal

Galton, por fin, introdujo el concepto de coeficiente de correlación lineal de Pearson. Curioso, ¿verdad? Curioso, digo, que lleve el nombre de Pearson. Como hemos dicho, Pearson fue su discípulo y precisó algunas deficiencias en la definición original de Galton. Con él podemos valorar la intensidad y el sentido de la relación lineal entre parejas de variables. El término correlación forma hoy en día parte de discusiones en ponencias y coloquios, en diversas áreas del conocimiento. Los datos estadísticos, que con frecuencia son tan difíciles de obtener, los conseguía en su laboratorio antropométrico inaugurado en la International Health Exhibition (Feria Internacional de la Salud) de 1884 y que mantuvo en funcionamiento durante 6 años en Londres. Este laboratorio le permitió recoger una colosal cantidad de datos y cobrar por los informes que realizaba. Un auténtico consulting estadístico que le convirtió en ser el primero capaz de cobrar a los sujetos experimentales. Su interés por la medición fue quizá la característica más notable de todas sus investigaciones. Lo medía todo de manera obsesiva. Era lo que en lenguaje coloquial llamaríamos hoy un auténtico friki. Un excéntrico. Y si no me creen, presten atención a algunas de sus inquietudes intelectuales diferentes de las relatadas hasta ahora. Juzguen ustedes.

Mapa de la belleza de las mujeres

En 1859, que ya no era un niño pues contaba con 37 años, se planteó con su primo Darwin (¡que tenía 50 años) obtener un mapa de belleza de las mujeres de las islas británicas. Hugh Aldersey-Williams en su libro Anatomías (Parra, 2013)

detalla cómo hacían para tomar los datos de manera discreta. No olvidemos que estamos en la Inglaterra victoriana. Para obtener los datos de lo que llamaba su “Mapa de la belleza”, cortaba un trozo de papel en forma de un crucifijo. Utilizando una aguja montada en un dedal, perforaba agujeros en el papel para clasificar las “muchachas junto a las que pasaba en las calles o en cualquier otro lugar, como atractivas, indiferentes o repelentes”. Los orificios para las chicas atractivas los hacía en la parte superior de la cruz, los correspondientes a las mujeres corrientes en el palo horizontal, y los de las feas en la base de la cruz. La ventaja de ello era que podía notar al tacto cada parte de la plantilla de papel en su bolsillo y registrar sus datos sin que las féminas de la ciudad que fuera le vieran ni sospecharan que las estaba evaluando. Como supongo estarán interesados en saber los resultados de un estudio tan peculiar que hoy cerraría un revista del corazón, hemos de decir que ganó Londres y cerró la clasificación Aberdeen, en el noreste de Escocia. Si sus mujeres no eran bellas para dichos primos, la ciudad es preciosa.

La eficacia de la oración

Otra de sus investigaciones más curiosas y que no estuvo exenta de polémica fue Statistical Inquiries into the efficacy of prayer (Investigaciones Estadísticas sobre la eficacia de la oración) de 1872. Galton trató de correlacionar los efectos de la oración con la duración de la vida. Como los clérigos se pasaban la vida orando y laborando, una mayor esperanza de sus vidas podía ser atribuida a los beneficios del rezo. Hay que recordar que Galton era profundamente religioso. Después de recopilar cientos de datos biográficos llegó a la conclusión de que las expectativas de vida de médicos y abogados eran mayores que las de los clérigos. Hay que decir en su honor que no manipuló los datos para obtener lo que él deseaba, práctica que no acaba de caer en desuso.

De la longitud de las condenas penales al agua de cada día y otros asuntos

También analizó diez mil sentencias de jueces de la corte británica para hacer una distribución de frecuencias de la longitud de las condenas. Además determinó con exactitud y utilizando complicadas fórmulas matemáticas respecto de la cantidad de agua que debía ingerirse en los diferentes momentos del día para estar perfectamente hidratado. Cuando asistía a las carreras de caballos, y lo hacía con frecuencia, obtenía distribuciones de frecuencias del cambio de color en la cara de los asistentes cuando los caballos se acercaban a la meta. Además diseñó un sombrero cuya parte superior se alzaba con una pera de goma permitiendo ventilar la cabeza en los días en los que el calor acosaba a los espectadores. Creó un índice de aburrimiento en los actos sociales, tan habituales en la Inglaterra victoriana. Concluyó que los asistentes atentos se sentaban erguidos mientras que los aburridos se movían constantemente de delante a atrás y la frecuencia de estos movimientos podía relacionarse con el aburrimiento. Para analizar las relaciones y afinidades entre sus invitados a casa, ideó un artilugio tipo sensor que, colocado bajo las sillas del salón, permitía cuantificar el número de veces que cada persona orientaba sus movimientos hacia cada uno de los demás. Es evidente que ya pensaba en las redes sociales, tan de moda ahora. También llevó a cabo estudios sobre el número de optimistas y pesimistas con cuestionarios apropiados a los que respondían los clientes de su laboratorio. En 1897 publicó nada más ni nada menos que en Nature un artículo estableciendo la longitud que debía tener la soga del ahorcado para fracturarle el cuello sin decapitarlo. Suena siniestro pero los intereses científicos en diferentes épocas han sido también muy distintos. A partir de los resultados de Galton y de otros científicos y con datos de ejecuciones fallidas, existe una tabla que relaciona peso del condenado con longitud de la soga. Y en la misma revista publicó un artículo sobre como cortar una tarta redonda de una manera científica. 

Su afán por descubrir características individuales de las personas le llevó a demostrar que personas diferentes tienen huellas dactilares diferentes. Inmediatamente este proceso de identificación, popular hoy en todo el mundo, fue adoptado por Scotland Yard y permitió resolver un elevado número de delitos pendientes en aquel momento. Ferviente defensor de las ideas de su primo, argumentó con tenacidad que las diferencias de aptitud en los seres humanos eran debidas a la herencia genética. Propuso un método de intervención social, la eugenesia, según el cual la reproducción debía planificarse para maximizar la inteligencia de los recién nacidos.

Socialmente debía aceptarse que los “eminentes” tuvieran muchos hijos y los demás menos. Figuras como Graham Bell, Bernard Shaw o Winston Churchill apoyaron sus ideas. Hoy en día se asocia el uso de ellas con el nazismo y otros regímenes totalitarios. Desde 1970 ningún país del mundo admite la eugenesia en sus políticas. 

Bien pues estas son algunas de las investigaciones de un tipo genial para la estadística del siglo XIX. Esperamos les halla gustado leer este pequeño articulo que fue rescatado de: (García & Corporativa, 2015)

        

            Referencias

 García, C. M. M., & Corporativa, U. C. de M. D. de E. e I. (2015). Momentos estelares de la probabilidad y de la estadística. Universidad Complutense, Departamento de Estudios e Imagen Corporativa. Consultado en: https://www.ucm.es/data/cont/docs/35-2019-02-04-3-2015-09-28-Lecci%C3%B3n%20Inaugural%202015-2016%20(Conrado%20Manuel%20Garc%C3%ADa).pdf , 6-05-2023.

                Francis Galton. (2023). En Wikipedia. https://en.wikipedia.org/w/index.php?title=Francis_Galton&oldid=1148926665 

Publicación: Solo para fines académicos, no persigue afanes de lucro-